Python für Data Science

Inhalt

Im achten Kapitel gehen wir wichtige Packages von Python für Data Science durch und decken die folgenden Konzepte ab:

Python für Data Science
numpy
Vektoren und Matrizen
Linear Algebra
Pandas Dataframes
Visualisieren von Daten
Graphen (G = (V, E))

Python für Data Science

Ein wichtiger Grund für die aktuelle Popularität von Python ist "Data Science", und die vielen Packages mit denen man in Python Daten verarbeiten und analysieren kann. Einen Überblick über beliebte Packages (nicht nur für Data Science) findet man zum Beispiel hier. Ein vollumfänglicher Überblick ist in diesem Rahmen weder möglich noch sinnvoll. Stattdessen werden Beispielhaft die Packages numpy, pandas und matplotlib aus dem SciPy Projekt, sowie das Package networkx, betrachtet. Weitere Packages, insbesondere Packages zur Datenanalyse und Modelbildung wie sklearn, statmodels und tensorflow können wir leider aus Zeitgründen nicht näher betrachten.

numpy

Der Kern des Packages numpy ist der Datentyp array für Vektoren und Matrizen. Auf der Grundlage von array stellt numpy Operationen für das wissenschaftliche Rechnen mit numerischen Daten zu Verfügung, von einfachen Berechnungen mit Matrizen, über lineare Alegebra, bis hin zu Fouriertransformationen. Auch Zufallsgeneratoren und einfache statistische Funktionen sind Teil von numpy.

Vektoren und Matrizen

Die Faustregel ist, dass in numpy alles vom Typ array ist (synonym für ndarray). Die Anzahl der Dimensionen bestimmt, ob es ein Vektor (1 Dimension), eine Matrix (2 Dimensionen), oder ein Tensor (mehr als zwei Dimensionen) ist. Man kann Vektoren und Matrizen einfach aus Listen oder anderen Sequenztypen erstellen. Es gibt außerdem noch einige nützliche Hilfsfunktionen, wenn man Vektoren und Matrizen mit bestimmen Mustern erstellen möchte.

Vektor mit numpy
>>> import numpy as np

>>> vector = np.array([1,2,3])
>>> # details for vector
>>> print(vector)
[1 2 3]

>>> # dimension of the array: 1 is a vector, 2 is a matrix, 3 upwards are tensors
>>> print("ndim:", vector.ndim)
ndim: 1

>>> # number of elements in the array
>>> print("size:", vector.size)
size: 3
>>> # dimensions of the array as a tuple with one entry per dimension
>>> print("shape", vector.shape)
shape (3,)

>>> matrix = np.array([[1,2,3],[4,5,6]])
>>> # details for matrix
>>> print(matrix)
[[1 2 3]
 [4 5 6]]

>>> print("ndim:", matrix.ndim)
ndim: 2

>>> print("size:", matrix.size)
size: 6

>>> print("shape", matrix.shape)
shape (2, 3)

>>> # creating a vector as a range
>>> vector_from_arange = np.arange(15)
>>> print(vector_from_arange)
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]

>>> # creating a lineary spaced sample
>>> print(np.linspace(0,1,100))
[0.         0.01010101 0.02020202 0.03030303 0.04040404 0.05050505
 0.06060606 0.07070707 0.08080808 0.09090909 0.1010101  0.11111111
 0.12121212 0.13131313 0.14141414 0.15151515 0.16161616 0.17171717
 0.18181818 0.19191919 0.2020202  0.21212121 0.22222222 0.23232323
 0.24242424 0.25252525 0.26262626 0.27272727 0.28282828 0.29292929
 0.3030303  0.31313131 0.32323232 0.33333333 0.34343434 0.35353535
 0.36363636 0.37373737 0.38383838 0.39393939 0.4040404  0.41414141
 0.42424242 0.43434343 0.44444444 0.45454545 0.46464646 0.47474747
 0.48484848 0.49494949 0.50505051 0.51515152 0.52525253 0.53535354
 0.54545455 0.55555556 0.56565657 0.57575758 0.58585859 0.5959596
 0.60606061 0.61616162 0.62626263 0.63636364 0.64646465 0.65656566
 0.66666667 0.67676768 0.68686869 0.6969697  0.70707071 0.71717172
 0.72727273 0.73737374 0.74747475 0.75757576 0.76767677 0.77777778
 0.78787879 0.7979798  0.80808081 0.81818182 0.82828283 0.83838384
 0.84848485 0.85858586 0.86868687 0.87878788 0.88888889 0.8989899
 0.90909091 0.91919192 0.92929293 0.93939394 0.94949495 0.95959596
 0.96969697 0.97979798 0.98989899 1.        ]

>>> # reshaping the elements of a vector into a matrix
>>> matrix_from_vector = vector_from_arange.reshape(3,5)
>>> print(matrix_from_vector)
[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]

>>> # zeros
>>> print(np.zeros( (3,5) ))
[[0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]]

>>> # ones
>>> print(np.ones( (3,5) ))
[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]

>>> # identity
>>> print(np.identity( 5) )
[[1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 1.]]

>>> # empty matrix without initialization (values cannot be predicted)
>>> print(np.empty( (3,5) ))
[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]

Der Zugriff auf array ist ähnlich wie bei anderen Datentypen in Python. Es gibt Indexzugriffe, man kann Slicing benutzen, sowie iterieren.

Matrix mit numpy
>>> import numpy as np
>>> matrix = np.linspace(0,1,100).reshape(10,10)
>>> # second row:
>>> print(matrix[2])
[0.2020202  0.21212121 0.22222222 0.23232323 0.24242424 0.25252525
 0.26262626 0.27272727 0.28282828 0.29292929]

>>> # second row:
>>> print(matrix[2,:])
[0.2020202  0.21212121 0.22222222 0.23232323 0.24242424 0.25252525
 0.26262626 0.27272727 0.28282828 0.29292929]

>>> # second column:
>>> print(matrix[:,2])
[0.02020202 0.12121212 0.22222222 0.32323232 0.42424242 0.52525253
 0.62626263 0.72727273 0.82828283 0.92929293]

>>> # rows 2-3, column 5-7
>>> print(matrix[1:3,4:7])
[[0.14141414 0.15151515 0.16161616]
 [0.24242424 0.25252525 0.26262626]]

>>> # first element in each row:
>>> for row in matrix:
...     print(row[0])
...
0.0
0.10101010101010102
0.20202020202020204
0.30303030303030304
0.4040404040404041
0.5050505050505051
0.6060606060606061
0.7070707070707072
0.8080808080808082
0.9090909090909092

Linear Algebra

Der große Vorteil von array gegenüber den Boardmitteln von Python sind die Funktionen für lineare Algebra, die weit über einfache Multiplikationen hinaus gehen.

Beispielprogramm von linearem Alegebra
>>> import numpy as np
>>> matrix = np.array([[1, 2], [3, 4]])

>>> # original matrix:
>>> print(matrix)
[[1 2]
 [3 4]]

>>> # transposed matrix:
>>> print(matrix.transpose())
[[1 3]
 [2 4]]

>>> # inverse of the matrix
>>> print(np.linalg.inv(matrix))
[[-2.   1. ]
 [ 1.5 -0.5]]

>>> # product of the matrix with itself
>>> print(matrix @ matrix)
[[ 7 10]
 [15 22]]

>>> # trace of the matrix, i.e., sum of diagonal
>>> print(np.trace(matrix))
5

>>> # determinant of the matrix
>>> print(np.linalg.det(matrix))
-2.0000000000000004

>>> # solution to the linear equation system matrix*x = [5,7]
>>> print(np.linalg.solve(matrix, np.array([5,7])))
[-3.  4.]

Pandas Dataframes

Mit numpy hat man ein mächtige Werkzeug zum Arbeiten mit Matrizen. Es gibt jedoch auch einige Aspekte, die man mit numpy nicht ohne weitere lösen kann, zum Beispiel:

Namen für Zeilen oder Spalten, sowie den Zugriff über den Namen.
Verschiedene Datentypen für Spalten, zum Beispiel Zeichenketten und numerische Daten.
Aggregationen und Join-Operationen, wie man sie von relationalen Datenbanken kennt.

Mit dem Package pandas wird diese Lücke geschlossen. Im Mittelpunkt von pandas stehen die Datentypen Series und DataFrame.

Eine Series ist ein 1-Dimensionaler Datentyp analog zu Vektoren, einzelnen Elemente können jedoch benannt sein.
Ein DataFrame ist ein 2-Dimensionaler Datentyp, ähnlich zu Matrizen. In einem Dataframe kann jedoch jede Spalte einen anderen Typ haben, außerdem können sowohl Zeilen, als auch Spalten, benannt sein.

Im folgenden Konzentrieren wir uns auf den Datentyp DataFrame.

1. Arbeiten mit Dataframes

Für pandas gilt, ähnlich wie für die Sprache Python, dass es viele Wege gibt, die selbe Aufgabe zu lösen. Hier sind nur einige Beispiele, wie man einen Dataframe erstellen kann.

Beispielprogramm Dataframes
>>> import numpy as np
# pandas is usually imported with the alias pd
>>> import pandas as pd

# initialize like numpy array
>>> df = pd.DataFrame([[1, 2], [3, 4]])
# initialize from numpy array
>>> df = pd.DataFrame(np.array([[1, 2], [3, 4]]))
>>> # data frame without names
>>> print(df)
   0  1
0  1  2
1  3  4

>>> # ...with names for rows and columns
>>> df = pd.DataFrame([[1, 2], [3, 4]], index=["row1", "row2"], columns=["col1","col2"])
>>> print(df)
      col1  col2
row1     1     2
row2     3     4

>>> # ...from a list of dictionaries:
>>> df = pd.DataFrame([{"col1": 1, "col2":2}, {"col1":3, "col2":4, "col3":5}])
>>> print(df)
   col1  col2  col3
0     1     2   NaN
1     3     4   5.0

>>> # ...from a dictionary of lists
>>> df = pd.DataFrame({"col1":[1,3], "col2":[2,4]})
>>> print(df)
   col1  col2
0     1     2
1     3     4

>>> df
   col1  col2
0     1     2
1     3     4

Intern basieren Dataframes auf numpy arrays. Über das values Attribut kann man einfach auf das numpy array zugreifen.

Zugriff auf numpy array in Dataframe
>>> df.values
array([[1, 2],
       [3, 4]])

Es gibt viele verschiedene Varianten, wie man auf Dataframes zugreifen kann. Der Zugriff auf Dataframes kann sowohl über die numerischen Spalten und Zeilenindizes geschehen, als auch über die Namen. Neben der Möglichkeit auf Spalten über den Namen, bzw. Reihen über Slicing direkt durch den [] Operator zuzugreifen, spielen die Methoden loc und iloc von Dataframes eine zentrale Rolle (kurzform von location, bzw. integer location), sowie die Methoden at und iat zum Zugriff auf einzelne Elemente.

Zugriff auf Panda Dataframe
>>> df = pd.DataFrame({"col1":[1,3,5], "col2":[2,4,6], "col3":["here","are","strings"]},
... index=["row1", "row2", "row3"])

>>> # access columns using the name
>>> print(df["col1"])
row1    1
row2    3
row3    5
Name: col1, dtype: int64

>>> # access  multiple columns using a list of names
>>> print(df[["col1", "col3"]])
      col1     col3
row1     1     here
row2     3      are
row3     5  strings

>>> # access a slice of rows
>>> print(df[0:2])
      col1  col2  col3
row1     1     2  here
row2     3     4   are

>>> # access row by name
>>> print(df.loc["row1"])
col1       1
col2       2
col3    here
Name: row1, dtype: object

>>> # access slice of rows by name
>>> print(df.loc["row1":"row2"])
      col1  col2  col3
row1     1     2  here
row2     3     4   are

>>> # slice of rows and columns
>>> print(df.loc["row1":"row2", "col1":"col2"])
      col1  col2
row1     1     2
row2     3     4

>>> # loc also supports lists of names
>>> print(df.loc[["row1","row3"], ["col1","col3"]])
      col1     col3
row1     1     here
row3     5  strings

>>> # iloc is the counterpart to loc that works with integers instead of names
>>> print(df.iloc[0:2,1:3])
      col2  col3
row1     2  here
row2     4   are

>>> # use at/iat to access single values (more efficient than loc/iloc)
>>> print(df.at["row1","col3"])
here

Dataframes können verändert werden. Man kann sowohl Spalten, als auch Zeilen, hinzufügen oder löschen.

Zugriff auf Panda Dataframe 2
>>> df = pd.DataFrame({"col1":[1,3], "col2":[2,4]}, index=["row1", "row2"])
>>> # add a new column using the name
>>> df["col3"] = [5,6]
>>> print(df)
      col1  col2  col3
row1     1     2     5
row2     3     4     6

>>> # assing a column to a specific position with insert
>>> df.insert(1, "col4", [7,8])
>>> print(df)
      col1  col4  col2  col3
row1     1     7     2     5
row2     3     8     4     6

>>> # delete a column using del
>>> del df["col2"]
>>> print(df)
      col1  col4  col3
row1     1     7     5
row2     3     8     6

>>> # add a new row
>>> # df.append([6,7,8]) is similar, but would not change df but create a new data frame
>>> df.loc["row3"] = [6,7,8]
>>> print(df)
      col1  col4  col3
row1     1     7     5
row2     3     8     6
row3     6     7     8

>>> # delete a row
>>> # inplace defines that the df is changed, with false a new data frame is created
>>> df.drop("row2", inplace=True)
>>> print(df)
      col1  col4  col3
row1     1     7     5
row3     6     7     8

2. Aggregieren und Mergen

Allein durch diese Arten des Zugriffs und die Vermischung von Zeichenketten und Zahlen bieten Dataframes schon wesentliche Vorteile gegenüber den numpy Matrizen. Ein weiterer Grund, warum Dataframes so beliebt sind, ist die Unterstützung von Aggregationsoperationen und Joins zum zusammenführen von Daten. Außerdem kann man Dataframes einfach aneinander anhängen, selbst wenn diese unterschiedliche Spalten haben.

Aggregationsoperationen auf Panda Dataframe
>>> import pandas as pd
>>> import numpy as np

>>> df = pd.DataFrame({'id':range(8),
...                    'A':['one', 'one', 'two', 'three',
...                        'two', 'two', 'one', 'three'],
...                     # creates a numpy array with random numbers
...                    'B': np.random.randn(8),
...                    'C': np.random.randn(8)})

>>> df2 = pd.DataFrame({'id':range(7,-1,-1),
...                     'D': np.random.randn(8),
...                     'E': np.random.randn(8)})

>>> # group by same values in column A and calculate the sum for each group
>>> print(df.groupby("A").sum())
       id         B         C
A
one     7 -0.874242  1.333538
three  10 -0.346491  1.907080
two    11  2.290283  1.923073

>>> # merge two data frames such that the rows that are equal in the 'on' column are combined
>>> print(pd.merge(df, df2, on="id"))
   id      A         B         C         D         E
0   0    one -0.352239  0.887510  2.043933 -0.700198
1   1    one  0.185039  0.656370 -1.450130  0.193392
2   2    two  1.264625  0.222088 -0.734909  0.035336
3   3  three  0.332399  1.095252 -1.031388  0.045444
4   4    two  1.020418  1.642165 -1.635857  0.091069
5   5    two  0.005241  0.058820 -1.670036 -0.139776
6   6    one -0.707042 -0.210341  0.341416 -2.835688
7   7  three -0.678890  0.811828 -1.339840  2.090281

>>> # concate two dataframes, missing columns are filled with NaN
>>> pd.concat([df, df2], sort=False)
   id      A         B         C         D         E
0   0    one -0.352239  0.887510       NaN       NaN
1   1    one  0.185039  0.656370       NaN       NaN
2   2    two  1.264625  0.222088       NaN       NaN
3   3  three  0.332399  1.095252       NaN       NaN
4   4    two  1.020418  1.642165       NaN       NaN
5   5    two  0.005241  0.058820       NaN       NaN
6   6    one -0.707042 -0.210341       NaN       NaN
7   7  three -0.678890  0.811828       NaN       NaN
0   7    NaN       NaN       NaN -1.339840  2.090281
1   6    NaN       NaN       NaN  0.341416 -2.835688
2   5    NaN       NaN       NaN -1.670036 -0.139776
3   4    NaN       NaN       NaN -1.635857  0.091069
4   3    NaN       NaN       NaN -1.031388  0.045444
5   2    NaN       NaN       NaN -0.734909  0.035336
6   1    NaN       NaN       NaN -1.450130  0.193392
7   0    NaN       NaN       NaN  2.043933 -0.700198

Fehlende Werte, die sich durch NaN in Dataframes widerspiegeln, kommen häufig vor. Der Umgang hiermit wird durch die Methoden dropna und fillna unterstützt.

Umgang mit NaN Werte
>>> import pandas as pd
>>> import numpy as np

>>> df = pd.DataFrame([{"col1": 1, "col2":2}, {"col1":3, "col2":4, "col3":5}])

>>> # drop all rows that contain a NaN
>>> print(df.dropna())
   col1  col2  col3
1     3     4   5.0

>>> # replace all NaN with a given value
>>> print(df.fillna(0))
   col1  col2  col3
0     1     2   0.0
1     3     4   5.0

3. Operationen auf Dataframes

Ein mächtiges Feature von pandas ist die Möglichkeit Operationen Zeilen, bzw. Spaltenweise auf Dataframes anzuwenden. Von Haus aus wird zum Beispiel die Berechnung von Mittelwerten und Standardabweichungen mitgeliefert. Man kann aber auch beliebige Funktionen hierfür definieren und anwenden. Hier kommen die in Kapitel 4 eingeführten Lambda Ausdrücke um anonyme Funktionen zu definieren wieder ins Spiel. Diese kann man nämlich auf Dataframes anwenden.

Operationen auf dataframes
>>> import pandas as pd
>>> import numpy as np

>>> df = pd.DataFrame({'A': np.random.randn(20),
...                    'B': np.random.randn(20),
...                    'c': np.random.randn(20)})

>>> # mean value of each column
>>> print(df.mean())
A   -0.231931
B    0.035385
c   -0.238496
dtype: float64

>>> # standard deviation of each column
>>> print(df.std())
A    1.066851
B    0.846248
c    0.995895
dtype: float64

>>> # difference between the 0.75 and 0.25 percentile for each column
>>> print(df.apply(lambda x: x.quantile(0.75)-x.quantile(.25)))
A    1.670910
B    0.785607
c    1.679432
dtype: float64

In den obigen Beispielen wurden die Operationen jeweils auf die Spalten eines Dataframes angewendet. Man kann die Operationen auch auf die Zeilen anwenden. Hierzu muss man die Achse (axis) definieren, auf der eine Operation angewendet werden soll. Es gibt zwei Achsen bei Dataframes: "index", bzw. 0 sind die Zeilen, "columns", bzw. 1 sind die Spalten. In der Regel wird die Achse 0 per Default genommen, das heißt die Operation läuft innerhalb einer Spalte entlang der Zeilen. Bei der Achse 1 wird innerhalb der Zeilen entlang der Spalten gelaufen. Um die Mittelwerte der Zeilen zu berechnen, muss man also als Achse 1, bzw. "columns" angeben.

Operationen auf dataframes 2
>>> # mean value of each row
>>> print(df.mean(axis=1))
   1.022864
   0.453551
  -0.025054
  -0.334792
  -0.291393
  -0.635646
  -0.004237
  -0.996640
  -0.438983
   0.203668
  0.416083
 -1.060859
 -0.555906
  0.414800
 -0.000369
  0.391112
 -1.099004
  0.672666
 -0.772999
 -0.259139
dtype: float64

4. Lesen und Schreiben von Dataframes

Bevor man mit Daten arbeiten kann, muss man diese erstmal einlesen. Wie man CSV Daten als Listen liest, haben wir bereits behandelt. Dataframes unterstützen auch das Lesen und Schreiben von CSV Dateien, ohne das man den Umweg über Listen gehen muss. Hierzu gibt es die Funktionen read_csv und to_csv.

Lesen vom dataframe
>>> import pandas as pd

>>> df = pd.read_csv("../python_examples/example.csv", header=None)
>>> df
    0          1        2                            3                          4          5
0  id  firstname lastname                        email                     email2 profession
1 100      Eadie      Pip        Eadie.Pip@yopmail.com        Eadie.Pip@gmail.com     worker
2 101 Fredericka    Hamil Fredericka.Hamil@yopmail.com Fredericka.Hamil@gmail.com     doctor
3 102    Maridel   Kellby   Maridel.Kellby@yopmail.com   Maridel.Kellby@gmail.com     doctor
4 103  Maryellen   Wandie Maryellen.Wandie@yopmail.com Maryellen.Wandie@gmail.com     doctor
5 104     Hayley   Mayeda    Hayley.Mayeda@yopmail.com    Hayley.Mayeda@gmail.com     worker

Visualisieren von Daten

1. Jupyter Notebook

Bisher wurde in allen Beispielen das Terminal verwendet, aber um die Daten zu visualisieren, muss ein Werkzeug verwendet werden, das Diagramme erstellen kann. Zu diesem Zweck wird die Online-Version von Jupyter Notebook, einem der am häufigsten verwendeten Werkzeuge für die Datenwissenschaft, verwendet. Benutzer, die es lokal installieren möchten, können sich auf die folgende Dokumentation beziehen.

Bei Jupyter Notebooks wird jedoch nicht für jede Ausführung einer Quelltextzelle der Interpreter neu gestartet. Stattdessen läuft der Interpreter dauerhaft im Hintergrund. Dies hat zur Folge, das Variablen nicht nur innerhalb einer Zelle gültig sind. Stattdessen ist eine Variable, die in einer Zelle definiert wurde, auch in allen anderen Zellen verfügbar. Die Zellen teilen sich also alle den gleichen Zustand. Das heißt, dass man auf der einen Seite Variablen wiederverwenden kann, auf der anderen Seite jedoch aufpassen muss, dass man nichts ungewollt überschreibt.

Der Interpreter wird mit jedem Start vom Notebook neu gestartet. Das heißt das direkt nach dem Start eines Notebooks keine Variablen verfügbar sind. Man kann den Interpreter auch über das Menü jederzeit neu starten, in dem man den Kernel des Notebooks neu lädt. Man kann beim Neustart des Kernels auch direkt die vorhandenen Ausgaben aus dem Notebook löschen.

Um eine neue Leerzeile in Jupyter notebook hinzuzufügen, wird einfach auf das Plus-Symbol geklickt und eine neue Zelle erscheint im Notebook.

2. Der erste Plot

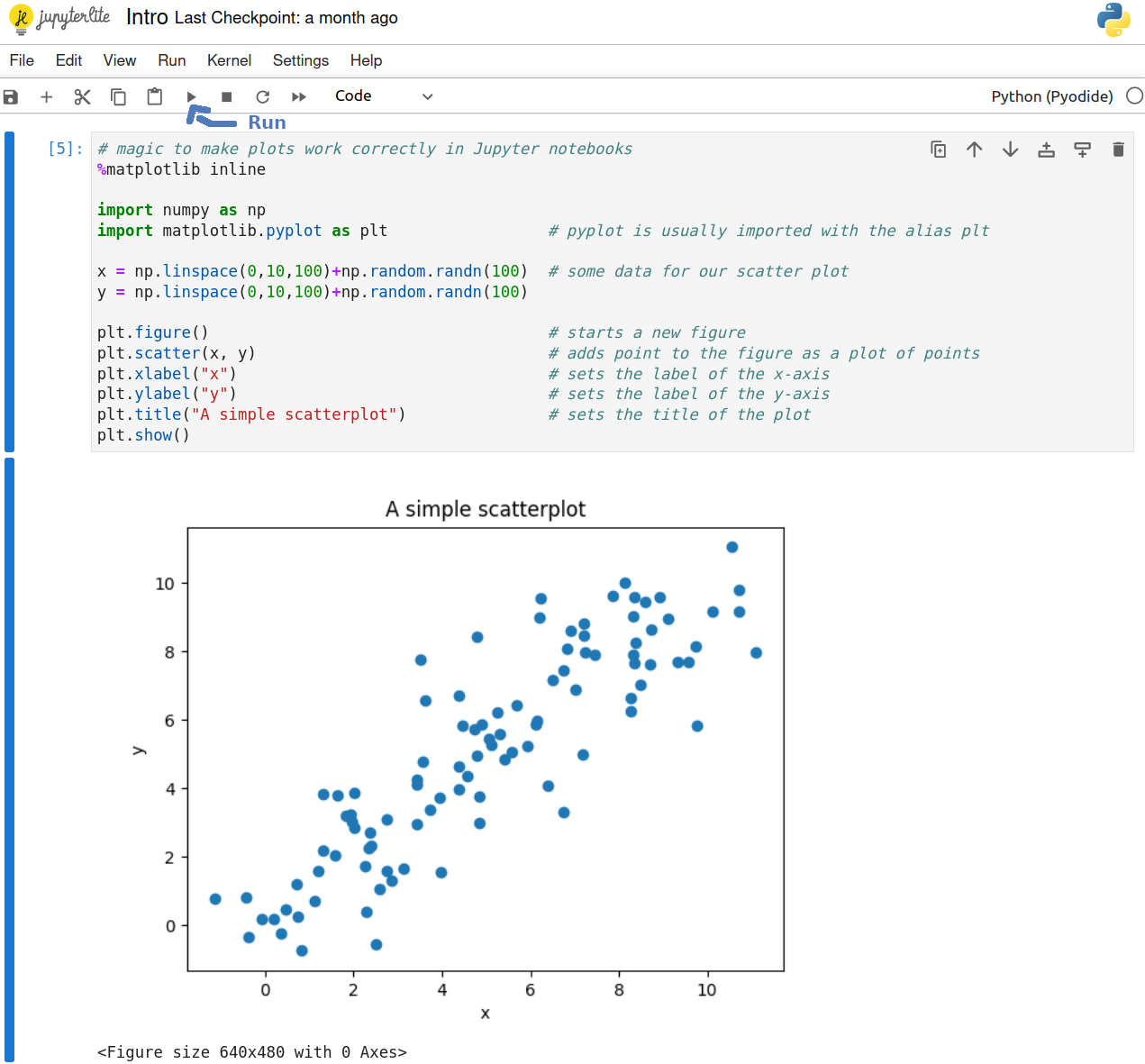
Das Package matplotlib ist ein sehr vielseitiges Package zum Erstellen von Grafiken. Wir betrachten matplotlib Anhand von Beispielen für die wichtigsten Visualisierungen.

Um mit matplotlib Grafiken zu erstellen, verwendet man pyplot. Mit pyplot erstellt man Grafiken nicht in einer einzigen, sehr mächtigen Anweisung. Stattdessen wird die Grafik durch eine Sequenz von Anweisungen definiert und intern in einem Zustandsautomaten verwaltet, bis die Ausgabe erfolgt. Grafiken (figures) werden in der Regel über plots erstellt, also Anweisungen was aufgetragen werden soll.

3. Übersicht über die Arten von Grafiken

Die Möglichkeiten von matplotlib sind riesig. In der Praxis ist es so, dass man sich überlegen sollte, welche Information man darstellen möchte und dann eine geeignete Grafik auswählt, die zu diesem Problem passt. Daher gibt es im folgenden nur einige Beispiele für Grafiken mit matplotlib. Scatterplots haben wir oben bereits gesehen. Scatterplots sind gut dafür geeignet, den Zusammenhang zwischen zwei Variablen darzustellen. Im folgenden gibt es noch Beispiele für Histogramme, Liniengrafiken, und Boxplots.

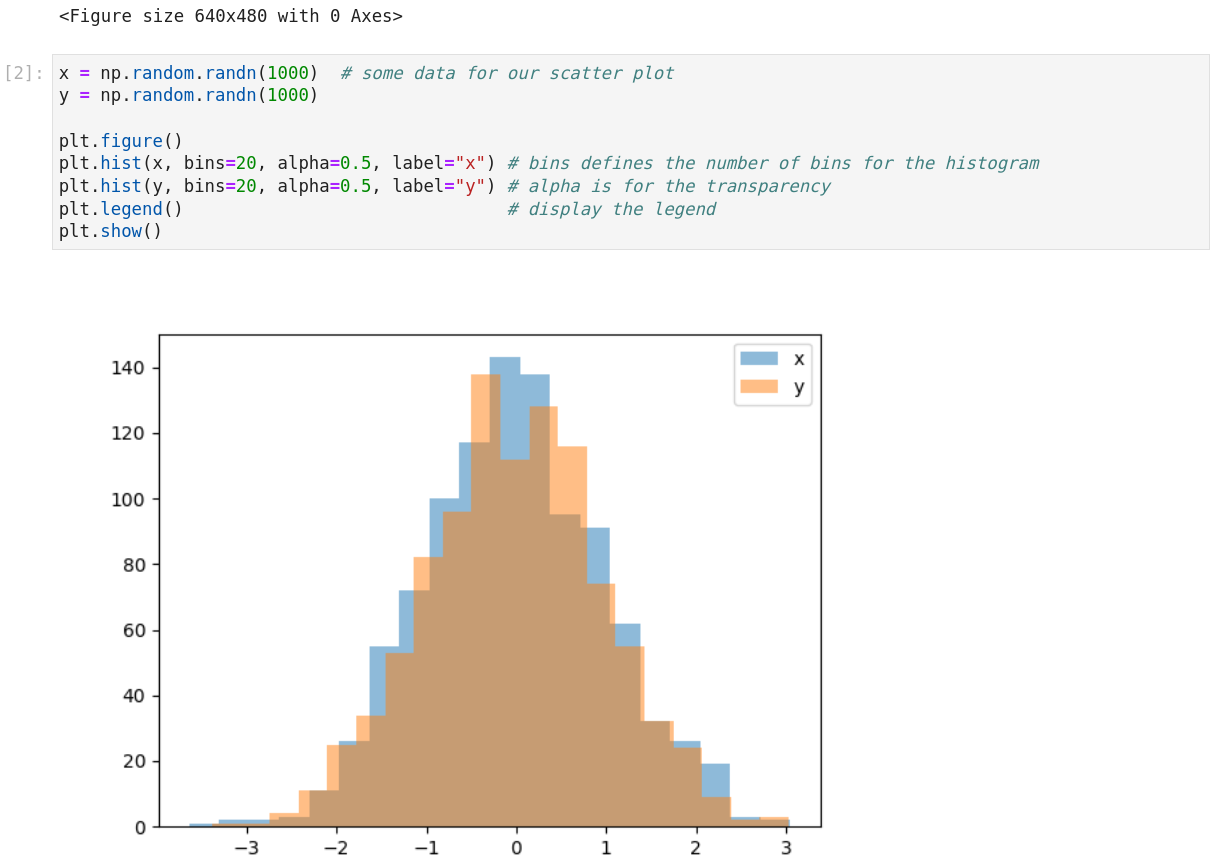
Will man wissen in welchem Bereich wie viele Daten sind, um zum Beispiel etwas über Wahrscheinlichkeitsverteilungen zu erfahren, sind Histogramme nützlich.

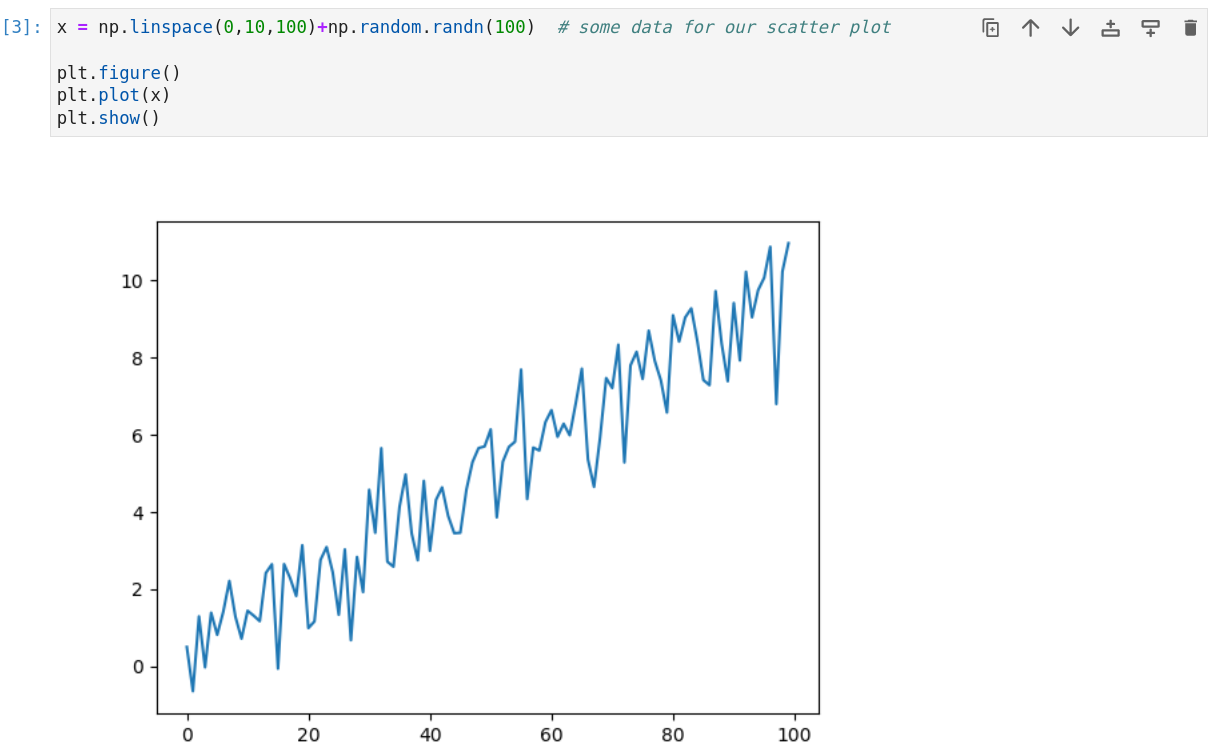
Liniengrafiken sind gut um den Verlauf zwischen Datenpunkten zu zeigen, zum Beispiel über die Zeit.

Boxplots sind gut geeignet, um etwas über die Verteilung von Daten auszusagen. Am besten hinterlegt man das ganze noch mit den echten Datenpunkten als jitter.

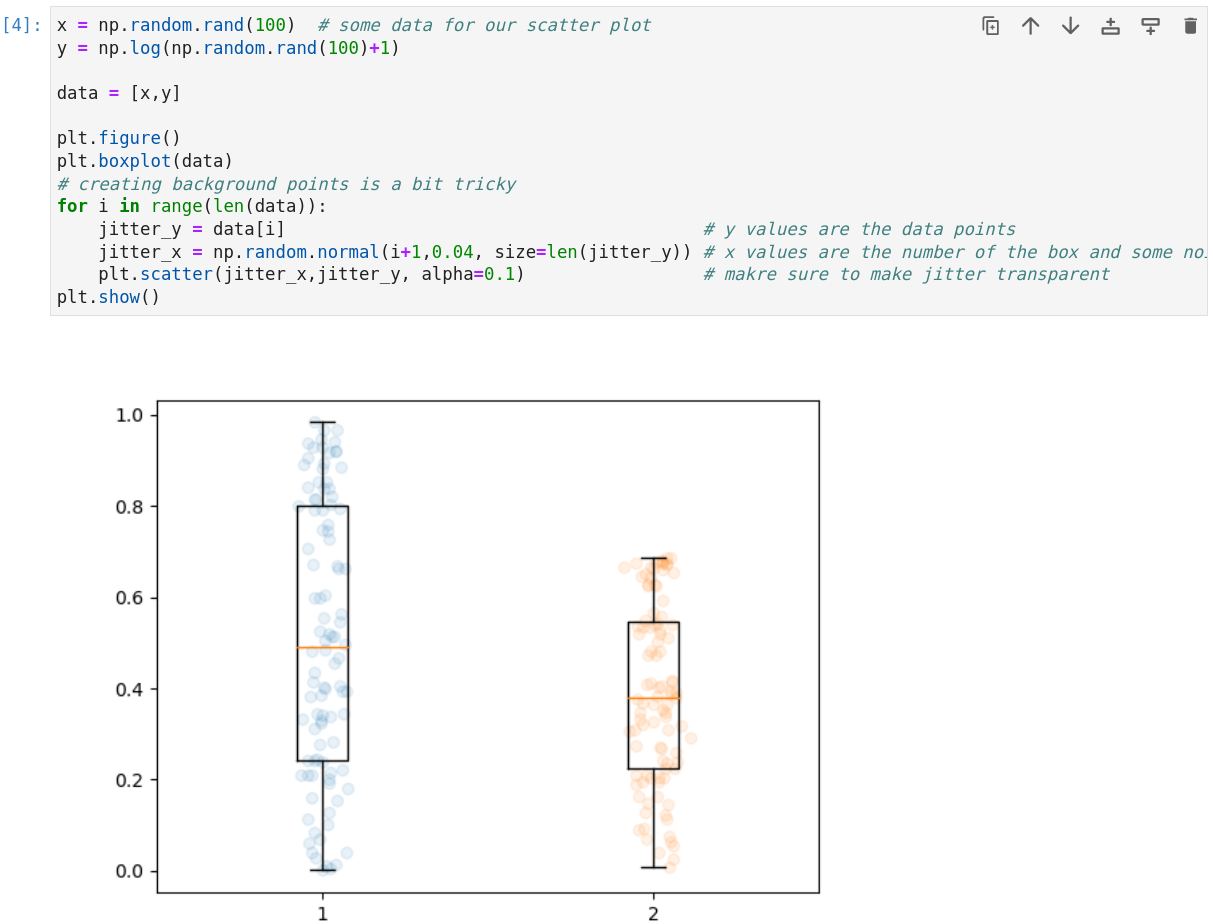Graphen

Graphen im mathematischen Sinne sind eine Datenstruktur G = (V, E), die aus Knoten (vertices) und Kanten (edges) besteht. Eine Kante zwischen zwei Knoten stellt eine Verbindung dar, die gerichtet oder ungerichtet sein kann. Graphen sind die Grundlage zur Analyse von Netzwerken, zum Beispiel von sozialen Netzwerken.

Eine beliebtes Package zum Arbeiten mit Graphen in Python ist networkx. Hiermit kann man einfach Graphen erstellen und mit vielen Algorithmen analysieren. Um einen Graphen zu erstellen, nutzt man einfach beliebige Python Objekte als Knoten und Tuple zwischen diesen Knoten als Kanten. Über Dictionaries kann man die Tupel erweitern und Attribute an den Knoten/Kanten speichern.

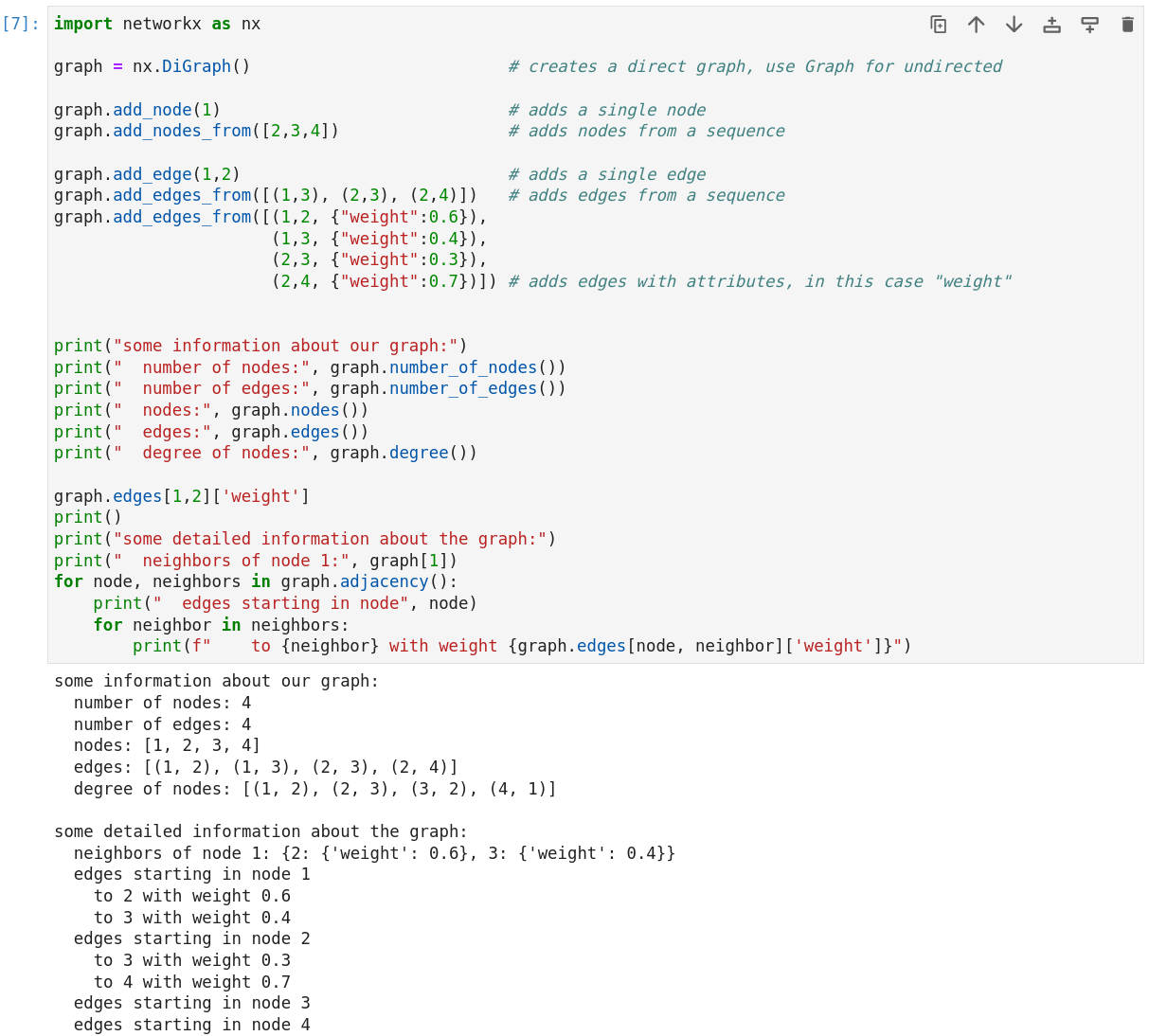Mit matplotlib kann man die Graphen einfach visualisieren.

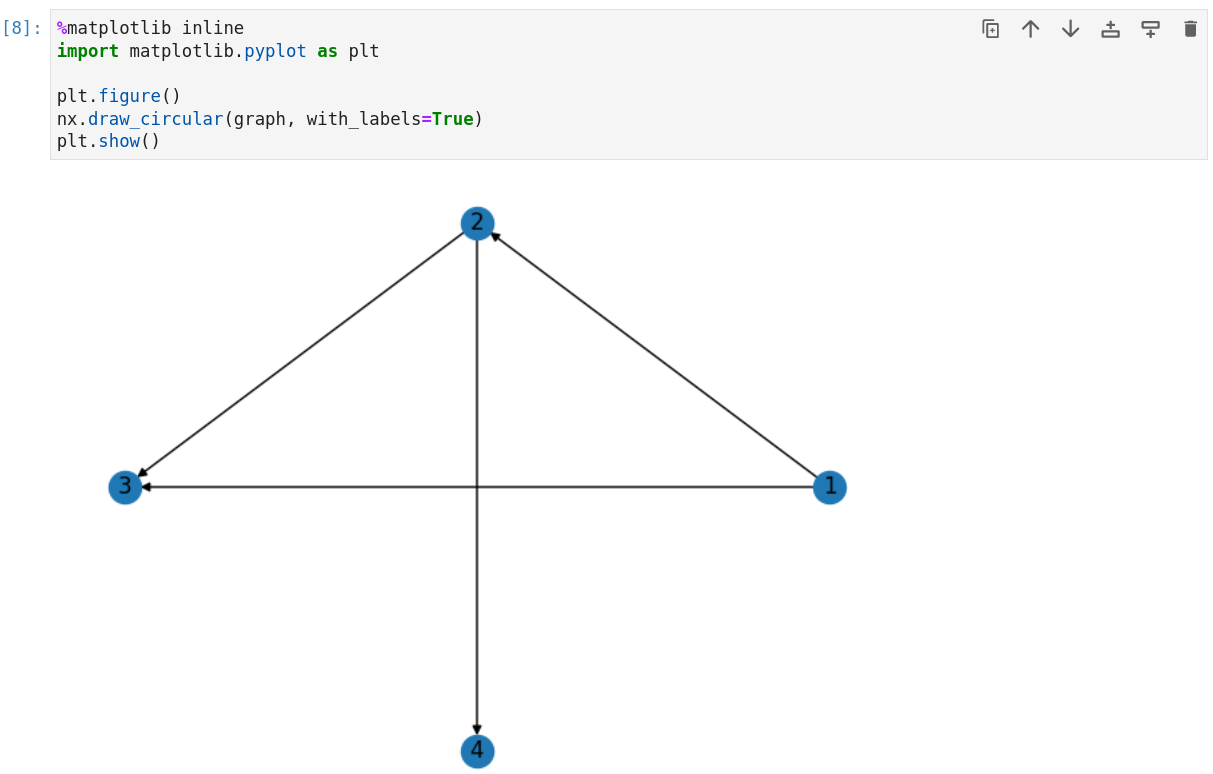networkx sorgt dafür, das Graphen konsistent bleiben. Löscht man einen Knoten, werden auch alle dazu gehörigen Kanten automatisch gelöscht.
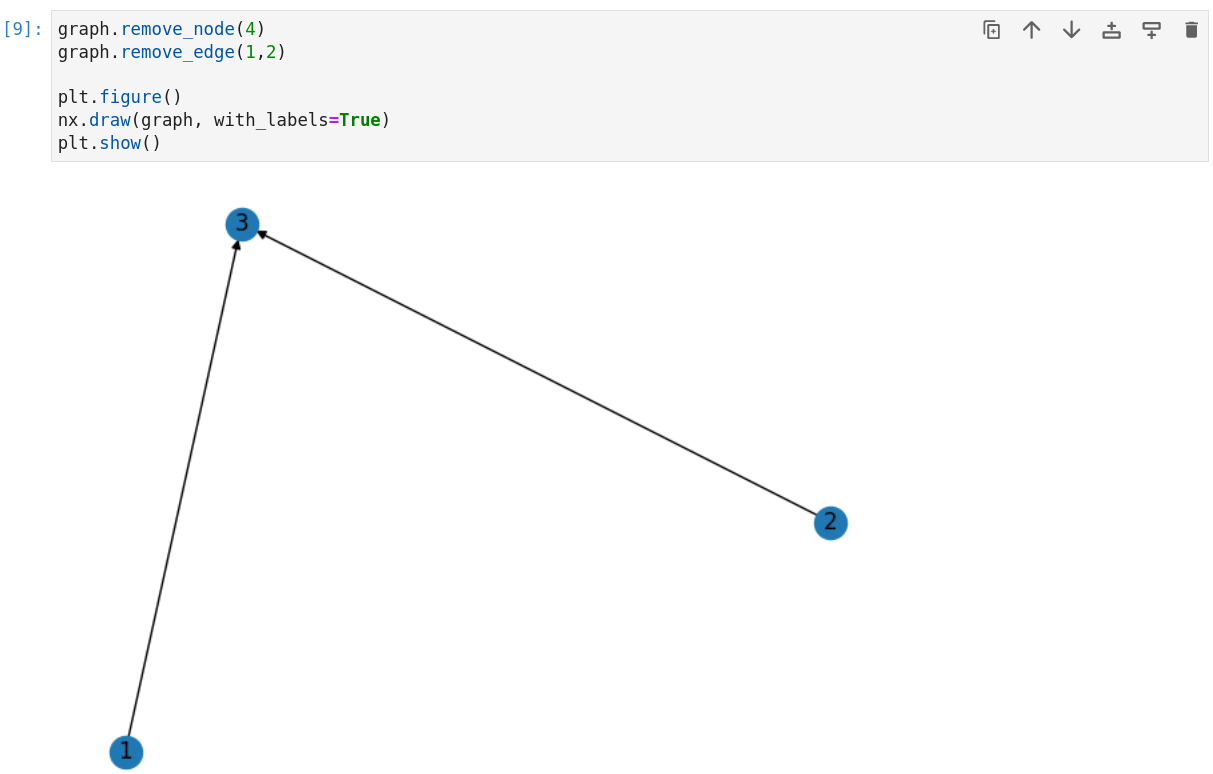